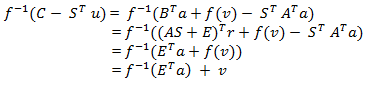1. Introduction

ecure transmission of data has become the key for successful completion of all transactions. NTRU Labs have created a bench-mark in secure transmission of data using a ring of truncated polynomials [1,2,3,4]. Many attempts have been made to break the crypto-systems based in NTRU technique; but no successful attempt has ever been reported. However polynomial inversions are difficult to perform in modulo-arithmetic. Moreover, polynomials are to be repeatedly chosen until they could be properly inverted.

In the last three to four years, Learning With Errors (LWE) has emerged as a versatile alternative to the NTRU cryptosystems. All cryptographic constructions based on LWE [5,6,7] are as secure as the assumption that SVP (Smallest Vector Problem) [8,9] is hard on integer lattices. The LWE problem can be stated as follows:

Recover s, given ?? . ?? ? ?? where ?? ? ?? ?? ?? , ?? ? ?? ?? ?? and A is m × n matrix with m > n and ?? ?? ?? is set of integer vectors of size n and modulo q. In other words, we are given a set of m equations in n unknowns and the right hand side slightly perturbed with the error vector chosen from normal distribution ? with low standard deviation. More precisely we say that an solves LWE [10] if we can recover s, given that the errors are distributed according to the error distribution ? and the elements of A are chosen uniformly at random from ?? ?? ?? [10].

The number of equations or the number of rows in the matrix is irrelevant since additional equations can be formed that are as good as new, by adding the given equations.

One way to obtain a solution to the LWE problem is to repeatedly form new equations until we get the first row of the matrix A as (1, 0, 0, 0, . . . ., 0) which gives a solution to the first component of s. We can repetitively apply the same procedure for the other components of s. However the probability of obtaining such a solution is almost nil, of the order of ?? ??? , and the set of equations needed are 2 ??(?? ?????? ??) and with a similar running time.

The algorithm can be stated as follows: Private Key: s, chosen uniformly at random from ?? ?? ?? .

Public Key: m samples of (A i , b i ). Encryption: for each bit of the message, we chose at However, transmitting a text with bitwise encryption will be cumber-some and time-taking. We use a slightly modified version of the algorithm to encrypt '??' bits simultaneously. We choose A, S uniformly at random from ?? ?? ?? ×?? and ?? ?? ??×?? respectively and S is the private key. We generate the error matrix ?? ? ?? ?? ??×?? by choosing each entry according to normal distribution???, where ? is a measure of standard deviation which is usually chosen as ????? and ? is small. The public key is (A, B) where B= A.S + E.

Farther simplification is made by choosing the elements of A in the form of a circulant matrix. In other words we have chosen A as [11] Let v be a vector belonging to message space ?? ?? ?? . Choose a vector ?? ? {???, ??, ??} ?? uniformly at random. The cipher text u corresponding to the message v is (?? = ?? ?? ??, ?? = ?? ?? ?? + ð??"ð??"(??)) where f is an invertible mapping from the message space ?? ?? ?? to ?? ?? ?? and in this paper we have chosen the mapping as a multiplication of each co-ordinate by ?? ?? ? and rounding to the nearest integer.

The original message can be recovered from the cipher text (u, C) using the private key S as ð??"ð??" ?1 (?? ? ?? ?? ??) which can be seen as follows:

If a decryption error is to occur, say in the first letter, the first co-ordinate of ?? ?? ?? must be greater than q (2t) ? in absolute value the probability of which is shown to be negligible [11].

However, some pre-processing of data greatly helps to reduce the time for encryption and decryption as well as time for transmission. We choose to compress the data before encryption using LZW (Lemple-Ziv-Welch) [12,13,14] technique and encrypt the reduced text. The LZW method of compression is based on dictionary structure. It creates a dictionary of its own for each character or a string of the input text. It is known to be a lossless compression and the percentage of reduction in the text is approximately 40% [15].

Another frequently used compression algorithm is the well known Huffman Technique [16,17,18] which constructs a binary tree based on the frequency of the occurrence of the letters and the corresponding code is generated. We have also used Huffman algorithm on the same text and compared the two compression technique used with LWE.

2. II.

3. Illustration of the Proposed Algorithm

The parameters of the proposed algorithm are chosen as ?? =2003, ?? =2, ?? =136, ?? =136, alpha = 0.0065 and ?? =2008 [11] Original text message str: wild animals, rocks, forest, beaches, and in general those things that have not been substantially altered by human intervention, or which persist despite human intervention.

4. Experimental Results

The following table gives the total execution time taken for a direct encryption and decryption, encryption and decryption after a LZW compression and encryption and decryption after a Huffman compression:

IV.

5. Conclusions

In this paper we have used ring-LWE to encrypt an input text. The text to be transmitted has been initially compressed using LZW Technique and the compressed text is encrypted using LWE. We have also used Huffman coding algorithm for compression for comparison purpose. It has been observed that compressing the input text greatly reduces the total time of transmission and Huffman coding works out to be better.

Author ? : Research Scholar, Department of Computer Science and Engineering, KLEF University, Vaddeswaram, Guntur, Andhra Pradesh, India. Author ?: Professor, Department of Electronics and Computer Engineering, KLEF University, Vaddeswaram, Guntur, Andhra Pradesh, India. Author ?: Professor Department of Computer Science and Engineering, Regency Institute of Technology, Yanam, U.T. of Podicherry, India. — Figure 1.

random a set T from the 2 m subsets of the m equations. The encryption is (? A ?? ????? , ? b ?? ????? ), if the bit is zero and the encryption is (? A ?? ????? , ? ?? + ? b ?? ????? ) if the bit is 1. Decryption: The decryption of the pair (a, b) is 0 if b -<a, s> is closer to 0 than to ? ?? , 1 otherwise. — Figure 2. 2 ? 2 ?

Compressed message using LZW is cmes= Where the integers indicate the indices to the patterns generated by the compression algorithm. Then we convert the message vector as obtained above into a binary v= ??( ??) = ð??"ð??"ð??"ð??"ð??"ð??"ð??"ð??"ð??"ð??"(?? × ?? ?? ) = ?? ? ?? ?? ?? × ð??"ð??" is chosen as ?? ? ?? ?? ð??"ð??" × ?? is as follows ?? ? ?? ?? ð??"ð??" × ?? is as follows ?? = ?? × ?? + ??(??ð??"ð??"ð??"ð??" ??) = Global Journal of Computer Science and Technology Volume XIV Issue VI Version I ?? = {???, ??, ??} ?? where the elements are chosen randomly. ?? = ?? ?? × ?? + ??(??)(??ð??"ð??"ð??"ð??" ??) = ð??"ð??" = ?? ?? × ?? (??ð??"ð??"ð??"ð??" ??) = ?? = ?? ? ?? ?? × ð??"ð??" (??ð??"ð??"ð??"ð??" ??) = D/(q/t) = Convert binary to decimalWhen the compression process is reversed we get the original message:III. — Figure 3. TheLet

Appendix A

Improving lattice based cryptosystems using the hermite normal form. D Micciancio . Lecture Notes in Computer Science J. Silverman (ed.) 2001. Mar. 2001. Springer-Verlag. 2146 p. .
Lattices in cryptography and cryptanalysis, D Micciancio . 2002. San Diego.
Worst-case to average-case reductions based on Gaussian measures. D Micciancio , O Regev . InProc. 45th Annual IEEE Symp. on Foundations of Computer Science (FOCS), 2004. p. .
Lattice-based cryptography. D Micciancio , O Regev . Post-quantum Cryprography, D J Bernstein, J Buch-Mann (ed.) 2008. Springer.
NTRUSIGN: Digital signatures using the NTRU lattice. J Hoffstein , N A H Graham , J Pipher , J H Silverman , W Whyte . Proc. of CT-RSA, Lecture Notes in Comput. Sci. (of CT-RSA) 2003. Springer-Verlag. 2612 p. .
Hybrid lattice reduction and meet in the middle resistant parameter selection for NTRUEncrypt. Submission/ contribution to ieee p1363, J Hoffstein , N Howgrave-Graham , J Pipher , J H Silverman . http://grouper.ieee.org/groups/1363/lattPK/submissions.html#2007-02 2007. NTRU Cryptosystems, Inc. 1.
NTRU: a ring based public key cryptosystem. J Hoffstein , J Pipher , J H Silverman . Proceedings of ANTS-III, (ANTS-III) June 1998. Springer. 1423 p. .
Algorithm 673 Dynamic Huffman Coding. J S Vitter . ACM Transactions on Mathematical Software June 1989. 1989. 15 (2) p. .
A Lossless Data Compression and Decompression Algorithm and Its Hardware Architecture. Ming-Bo Lin , Jang-Feng Lee , G E Jan . VLSI IEEE Transactions 2006. 14 p. .
NTRU Encryption using Huffman comprssion. M N M Prasad , Mohammed Ali Hussain , C V Sastry . Journal of Theoretical and Applied Information Technology Jan 2014. 59 (2) p. .
Tensor-based hardness of the shortest vector problem to within almost polynomial factors. O Haviv , Regev . Proc. 39th ACM Symp. on Theory of Computing (STOC), (39th ACM Symp. on Theory of Computing (STOC)) 2007. p. .
On lattices, learning with errors, random linear codes, and cryptography. O Regev . J.ACM 2009. 56 (6) .
Enhancing LZW Algorithm to Increase Overall Performance. Parvinder Singh , Priyanka Manojduhan . Annual IEEE Indian Conference, 2006. p. .
Introduction to Data Compression, R Mateosian . 1996. 16.
Coding available at http:// www, Salomon D Huffman . 2008. Softcover.
Hardness of approximating the shortest vector problem in lattices. S Khot . Proc. 45th Annual IEEE Symp. on Foundations of Computer Science (FOCS), (45th Annual IEEE Symp. on Foundations of Computer Science (FOCS)) 2004. p. .
Design and Implementation of LZW Data Compression Algorithm. V Sulochana Verma . IJIST vol2, July 2012.

LWE Encryption using LZW Compression

Table of contents