Fuzzy Reinforcement Learning using Neural Network: An Application to Medical Diagnosis and Business Intelligence

Table of contents

1. Introduction

nformation available to many applications like Business, Medical, Geological, Control Systems, etc is incomplete or uncertain. The fuzzy logic will deal with incomplete information with belief rather than likelihood (probable). Zadeh formulated uncertain information as fuzzy set with a single membership functions. The fuzzy set with two membership functions will give more evidence than a single membership function. The two-fold fuzzy set is with fuzzy membership functions "Belief" and "Disbelief". Usually, in Medical and Business applications, there are two opinions like "Belief" and "Disbelief" about the information and decision has to be taken under risk. For instance, in Mycin [1], the medical information is defined with belief and disbelief i.e.

2. /, CF[h,e]=MB[h,e] -MD[h.e],

where "e" is the evidence for given hypothesis "h". The fuzzy set is used instead of Probability to define fuzzy certainty factor.

The fuzzy neural networks are one of the learning techniques to study fuzzy problems. In the following, some methods of fuzzy conditional inference are studied through fuzzy neural network and before that preliminaries of fuzzy logic and neural network are discussed.

In the following fuzzy logic [10] and Generalized fuzzy logic [9] are studied briefly. The fuzzy Certainty Factor is studied and fuzzy Decision set is proposed. The fuzzy inference and fuzzy reasoning are studied for fuzzy Decision set. The Business applications are studied as applications of fuzzy Decision set.

Author: e-mail: [email protected] II.

3. Fuzzy Logic

Various theories are studied to deal with imprecise, inconsistent and inexact information and these theories deal with likelihood whereas fuzzy logic with belief. Zadeh [10] has introduced fuzzy set as a model to deal with uncertain information as single membership functions. The fuzzy set is a class of objects with a continuum of grades of membership. The set A of X is characterized by its membership function µA(x) and ranging values in the unit interval For instance "Rama has mild headache" with Fuzziness 0.4

[0, 1]. µA(x): X ?[0, 1], x ? X,

The fuzzy logic is defined as combination of fuzzy sets using logical operators [21]. Some of the logical operations are given below Let A, B and C are fuzzy sets. The operations on fuzzy sets are

Negation If x is not A A'=1-µ A (x)/x

4. Conjunction

x is A and y is B? (x, y) is A x B A x B=min(µ A (x)), µ B (y)}(x,y)

5. If x=y

x is A and y is B? (x, y) is A?B

A?B=min(µ A (x)), µ B (y)}/x x is A or y is B? (x, y) is A' x B' A' x B' =max(µ A (x)), µ B (y)}(x,y) If x=y x is A and x is B? (x, x) is A V B AVB=max(µ A (x)), µ B (y)}/x Disjunction Implication If x is A then y is B =A?B = min{1, 1-µ A (x)) +µ B (y)}/(x,y) if x= y A?B= min {1, 1-µ A (x)) +µ B (y)}/x If x is A then y is B else y is C= A x B + A' x C

The fuzzy proposition "If x is A then y is B else y is C" may be divided into two clause "If x is A then y is B " and "If x is not A then y is C"

[15] If x is A then y is B else y is C =A?B= min {1, 1-µA(x)+ µB(y)}/(x,y) If x is not A then y is B else y is C =A'? C = min {1, 1-µ A (x)) +µ C (y)}/(x,y) Composition A o B= A x B=min{ µ A (x)), µ B (y)}/(x,y) If x = y A o B==min{ µ A (x)), µ B (y)}/x Composition

The fuzzy propositions may contain quantifiers like "Very", "More or Less". These fuzzy quantifiers may be eliminated as

Concentration x is very A µ very A (x)), =µ A (x) ²

6. Diffusion

x is very A µ more or less A (x) =µ A (x) 0.5

7. III. Generalized Fuzzy Logic with two-Fold Fuzzy Set

Since formation of the generalized fuzzy set simply as two-fold fuzzy set and is extension Zadeh fuzzy logic. The fuzzy logic is defined as combination of fuzzy sets using logical operators. Some of the logical operations are given below Suppose A, B and C are fuzzy sets. The operations on fuzzy sets are given below for two-fold fuzzy sets.

Since formation of the generalized fuzzy set simply as two-fold fuzzy set, Zadeh fuzzy logic is extended to these generalized fuzzy sets.

Negation A?= {1-µ A Belief (x), 1-µ A Disbelief (x) }/x Disjunction AVB={ max(µ A Belief (x) , µ A Belief (y)), max(µ B Disbelief (x) , µ B Disbelief (y))}(x,y) Conjunction A?B={ min(µ A Belief (x) ,µ A Belief (y)), min(µ B Disbelief (x) , µ B Disbelief (y)) }/(x,y) Implication A?B= {min (1, 1-µ A Belief (x) + µ B Belief (y) , min ( 1, 1-µ A Disbelief (x) + µ B Disbelief (y)}(x,y) If x is A then y is B else y is C = A x B + A' x C If x is A then y is B else y is C =A?B = {min (1, 1-µ A Belief (x) + µ B Belief (y) , min ( 1, 1-µ A Disbelief (x) + µ B Disbelief (y)}/(x,y) if `A If x is not A then y is B else y is C =A??C = min (1, µ A Belief (x) + µ C Belief (y) , min (1,µ A Disbelief (x) + µ C Disbelief (y)}(x,y) Composition A o R= {min x ( µ A Belief (x), µ A Belief (x) ), min x ( µ R Disbelief (x), µ R Disbelief (x) )}/y

The fuzzy propositions may contain quantifiers like "very", "more or less". These fuzzy quantifiers may be eliminated as

Concentration "x is very A µ very A (x) = { µ A Belief (x) 2 , µ A Disbelief (x)µ A (x) 2 }

Diffusion "x is more or less A" µ more or less A (x) = ( µ A Belief (x) 0.5 , µ A Disbelief (x)µ A (x) 0.5

For instance, Let A, B and C are A = { 0.8/x 1 + 0.9/x 2 + 0.7/x 3 + 0.6/x 4 +0.5/x 5 , 0.4/x 1 + 0.3/x 2 + 0.4/x 3 + 0.7/x 4 +0.6/x 5 } B = { 0.9/x 1 + 0.7/x 2 + 0.8/x 3 + 0..5/x 4 +0.6/x 5 , 0.4/x 1 + 0.5/x 2 + 0.6/x 3 + 0.5/x 4 +0.7/x 5 } A V B = { 0.9/x 1 + 0.9/x 2 + 0.

8. Fuzzy Neural Network

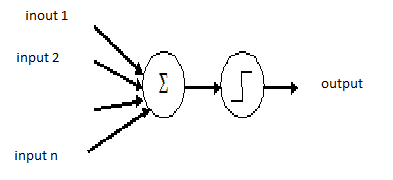
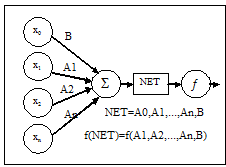
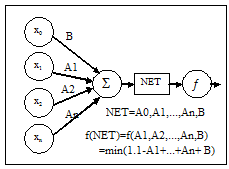
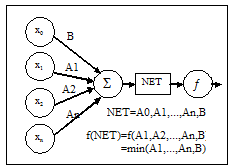
The neural network concept is taken from the Biological activity of nervous system. The neurons passes information to other neurons. There are many models described for neural networks. The McCulloch-Pitts model contributed in understanding neural network and Zedeh explain that activity of neuron is fuzzy process [13].

The McCulloch and Pitt's model consist of set of inputs, processing unit and output and it is shown in Fig.

9. Fuzzy Decision Set

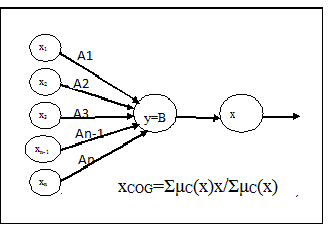
Zadeh [10] proposed fuzzy set to deal with incomplete information. Generalized fuzzy set with two-fold membership function µ A (x ) = { µ A Belief (x ) , µ A Disbelief (x ) } is studied [18] The fuzzy Certainty Factor may be defined as (FCF) The Generalized fuzzy set for Demand for the Items and fuzzy certainty factor is shown in Fig5. Decision may be taken under Decision shown in Fig. 6.

µ A FCF (x ) = µ A Belief (x ) -µ A Disbelief (x ) , where µ A FCF (x) = µ A Belief (x) -µ A Disbelief (x) µ A Belief (x) ?µ A Disbelief (x) = 0 µ A Belief (x) <µ A Disbelief (x)

10. Fig. 6: Fuzzy Decision set

The fuzzy logic is combination of logical operators. Consider the logical operations on fuzzy Decision sets r1, R2 and R3

Negation If x is not R1 ( ) D Year 2021 R1'=1-µ R1 (x)/x Conjunction x is R1 and y is R2? (x, y) is R1 x R2 R1 x R2=min(µ R1 (x)), µ R2 (y)}(x,y) If x=y x is R1 and y is R2? (x, y) is R1?R2 R1?R2=min(µ R1 (x)), µ R2 (y)}/x x is R1 or y is R2? (x, y) is R1' x R2' R1' x R2' =max(µ R1 (x)), µ R2 (y)}(x,y) If x=y x is R1 and x is R2? (x, x) is R1 V R2 R1VR2=max(µ R1 (x)), µ R2 (y)}/x Disjunction Implication if x is R1 then y is R2 =R1?R2 = min{1, 1-µ R1 (x)) +µ R2 (y)}/(x,y) if x= y R1?R2= min {1, 1-µ R1 (x)) +µ R2 (y)}/x Composition R1 o R2= R1 x R2=min{ µ R1 (x)), µ R2 (y)}/(x,y) If x = y R1 o R2==min{ µ R1 (x)), µ R2 (y)}/x

The fuzzy propositions may contain quantifiers like "Very", "More or Less". These fuzzy quantifiers may be eliminated as

11. Concentration

12. Fuzzy Conditional Infrence in Decision Making

Decision management is usually happens in Decision Support Systems.

13. Conclusion

The decision has to be taken under incomplete information in many applications like Business, Medicine etc. The fuzzy logic is used to deal with incomplete information The fuzzy Decision set is defined with twofold fuzzy set. The fuzzy logic is discussed with two-fold fuzzy set. The fuzzy Decision set, inference and reasoning are studied. The Business applications is discussed for fuzzy Decision set.

Figure 1. Fig. 1 :
1Fig. 1: fuzzy membership functionThe fuzzy set of type 2 "Headache" is defined as Headache = {0.4/mild + 0.6/moderate+ 0.8/Serious} For example, consider the fuzzy proposition "x has mild Headache"
Figure 2. 2
2
Figure 3. Fig. 2 :
2Fig. 2: McCulloch and Pitt's model The fuzzy neuron model for fuzzy conditional inference for If x 1 is A 1 and/or x 2 is A 2 and/or ? and/or x n is A n then B may be defined as set of individuals of the universe of discourse, fuzziness and computational functional function and shown in Fifg.3. Where B=f(A 1 ,A 2 ,?A n )This fuzzy neuron fit for where the relation between president part and consequent part of fuzzy conditional inference is not known
Figure 4. Fig. 3 : 4 Fig
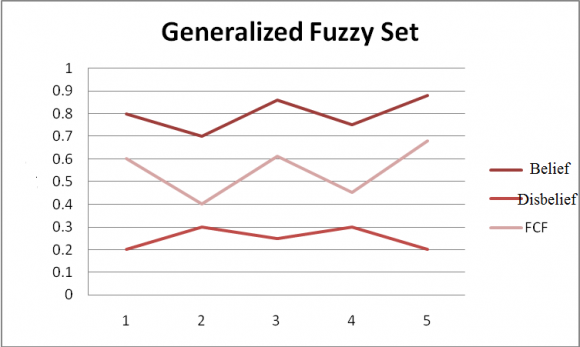
34Fig. 3: Fuzzy neuron modelThe multilayer fuzzy neural net work is shown in Fig.3The fuzzy neuron for Defuzzification for Centre of Gravity (COG) is shown in fig.4
Figure 5. Fuzzy
Decision set R is defined based on convex fuzzy set [10] R= {A , µ A FCF (x )??}, where ??[0,1] For instance, Demand ={ 0..8/x1+0.7/x2+0.86/x3+0.75/x4+0.88/x5, 0.2/x1+0.3/x2+0.25/x3+0.3/x4+0.2/x5 } µ Demand FCF (x ) = 0.6/x1+0.4/x2+0.61/x3+0.45/x4+0.68/x5
Figure 6. Fig. 5 :
5Fig. 5: Generalized fuzzy set
Figure 7. x 7 Fig. 7 : 8 Fig. 8 : 9 Fig. 9 :
778899Fig. 7: Zadeh fuzzy conditional inference
Figure 8.
Young={.95/10+0.9/20+0.8/30+0.6/40+0.4/50+0.3/6
0+0.2/70+0.15/80+0.1/90}
Not young={ 0.05/10 + 0.1/20 + 0.2/30+0.4/40
+0.6/50 + 0.8/60+0.7/70 +0.95/80+0.9/90 }
For instance "Rama is young" and the fuzziness
of "young" is 0.8 The Graphical representation of young
and not young is shown in fig.1
Note: A = µA(x1)/x1 + µA(x2)/x2 + ? + µA(xn)/xn, "+" is unionFor example, the fuzzy proposition "x is young"
Figure 9.
0.16/x 1 + 0.09/x 2 + 0.16/x 3 + 0.49/x 4 +0.36/x 5
µ More or Less A (x) = ( µ A Belief (x) 1/2 , µ A Disbelief (x)µ A (x) 1/2 }
= { 0IV.
Year 2021
8/x 3 + 0.6/x 4 +0.6/x 5 , 0.4/x 1 + 0.5/x 2 + 0.6/x 3 + 0.7/x 4 +0.7/x 5 } A ? B = { 0.8/x 1 + 0.7/x 2 + 0.7/x 3 + 0.5/x 4 +0.5/x 5 , 0.4/x 1 + 0.3/x 2 + 0.4/x 3 + 0.5/x 4 +0.6/x 5 } A' = not A= { 0.2/x 1 + 0.1/x 2 + 0.3/x 3 + 0.4/x 4 +0.5/x 5 , 0.6/x 1 + 0.7/x 2 + 0.6/x 3 + 0.3/x 4 +0.4/x 5 } A? B = { 1/x 1 + 0.8/x 2 + /x 3 + 0.9/x 4 +1/x 5 , 1/x 1 + 1/x 2 + 1/x 3 + 0.8/x 4 +1/x 5 } A o B = { 0.8/x 1 + 0.7/x 2 + 0.7/x 3 + 0.5/x 4 +0.5/x 5 , 0.4/x 1 + 0.3/x 2 + 0.4/x 3 + 0.5/x 4 +0.6/x 5 } = { µ A Belief (x) 2 , µ A Disbelief (x)µ ( ) µ Very A (x) D
Note: A (x) 2 } = { 0.64/x 1 + 0.81/x 2 + 0.49/x 3 + 0.36/x 4 +0.25/x 5 ,
Figure 10.
Zadeh inference is given as A?B= min{1, 1-µ A (x) + µ B (x)}
µ Demand ? High Price FCF (x ) = 0.9/x1+1/x2+0.5/x3+1/x4+0.52/x5
µ Demand ? High Price FCF (x ) ?0.6 = 1/x1+1/x2+0/x3+1/x4+0/x5
Mamdani inference is given as A?B= min{µ A (x) , µ B (x)}
µ Demand ? High Price FCF (x ) = 0.4/x1+.44/x2+0.29/x3+.33/x4+0.2/x5
µ Demand ? High Price FCF (x ) ?0.6 = 1/x1+1/x2+0/x3+1/x4+0/x5
Mamdani inference is given as A?B= min{µ A (x) }
Year 2021 Example 2 µ Demand ? High Price µ Demand ? High Price FCF (x ) = 0.4/x1+.44/x2+0.29/x3+.33/x4+0.2/x5 FCF (x ) ?0.6 = 1/x1+1/x2+0/x3+1/x4+0/x5
Consider Medical Diagnosis
If x has infection in the leg then surgery
Let x1, x2, x3, x4, x5 are the Patients.
The fuzzy set
µ Infection FCF (x ) = 0.76/x1+0.78/x2+0.46/x3+0.86/x4+0.58/x5,
0.16/x1+0.12/x2+0.06/x3+0.14/x4+0.05/x5}
= 0.6/x1+0.64/x2+0.4/x3+0.72/x4+0.53/x5
µ Surgery FCF (x ) = 0.59/x1+0.26/x2+0.55/x3+0.24/x4+0.35/x5,
0.09/x1+0.06/x2+0.05/x3+0.04/x4+0.03/x5 }
= 0.5/x1+0.2/x2+0.5/x3+0.2/x4+0.32/x5
( ) D Using inference rule A?B= min{1, 1-µ A (x) + µ B (x)}
µ Infection ? Surgery FCF (x ) = 0.9/x1+0.56/x2+0.9/x3+1/x4+1/x5
µ Infection ? Surgery R (x ) = 1 µ Infection ? Surgery FCF (x ) ?6
0 µ Infection ? Surgery FCF (x ) <6
The fuzzy risk set R is
1/x1+0/x2+1/x3+1/x4+1/x5
Example 1 µ Infection ? Surgery FCF (x ) = 0.9/x1+0.56/x2+0.9/x3+1/x4+1/x5
Consider Business rule µ very Surgery FCF (x ) = 0.25/x1+0.2\04/x2+0.25/x3+0.04/x4+0.1/x5
If x is Demand of the product then x is High Price Let x1, x2, x3, x4, x5 be the Items. x is very Demand o Demand?Increase Price
The Generalized fuzzy set =0.35/x1+0.66/x2+0.35/x3+0.04/x4 + 0.1/x5
Demand ={ 0.56/x1+0.48/x2+0.86/x3+0.36/x4+0.88/x5, 0.06/x1+0.04/x2+0.07/x3+0.03/x4+0.2/x5 }
VII. µ Demand FCF (x ) = 0.5/x1+0.44/x2+0.79/x3+0.33/x4+0.68/x5
High Price = 0.49/x1+0.52/x2+0.35/x3+0.4/x4+0.3/x5,
0.09/x1+0.02/x2+0.06/x3+0.02/x4+0.1/x5 }
µ High Price FCF (x ) = 0.4/x1+0.5/x2+0.29/x3+0.38/x4+0.2/x5
1
2
3

Appendix A

  1. Rule-Based Expert System: The MYCIN Experiments of the Stanford Heuristic Programming Project, Readings, B G Buchanan , E H Shortliffe . 1984. Addition-Wesley, M.A.
  2. An experiment in linguistic synthesis with a fuzzy logic control. E H Mamdani , S Assilian . International Journal of Man-Machine Studies 1975. 7 (1) p. .
  3. , G Shafer , Mathematical . 1976. Princeton, NJ: University Press.
  4. Fuzzy Logic, Neural Networks and Soft Computing. L A Zadeh . Communications of ACM 37 (3) p. .
  5. L A Zadeh . fuzzy sets, In Control, 1965. 8 p. .
  6. Generalized theory of uncertainty (GTU)-principal concepts and ideas Computational Statistics & Data Analysis, L A Zadeh . 2006. 51 p. .
  7. In fuzzy set s and their Applications to Cognitive and Decision Processes, L Zadeh . L. A. Zadeh, King-Sun FU, Kokichi Tanaka and Masamich Shimura (ed.) 1975. New York: Academic Press. p. . (Calculus of fuzzy Restrictions)
  8. Many-Valued Logic, N Rescher . 1969. New York: McGrow-Hill.
  9. Some Methods of Reasoning for Conditional Propositions. Poli Venkata , Subba Reddy , M. Syam Babu . fuzzy set s and Systems, 1992. 52 p. .
  10. Generalized fuzzy logic for Incomplete Information. Poli Venkata , Subba Reddy . IEEE International Conference on fuzzy Systems, (Hyderabad, India
    ) July 7-10, 2013.
  11. Fuzzy Conditional Inference for Medical Diagnosis. P Venkata Subba , Reddy . Proceedings of Second International Conference on Fuzzy Theory and Technology, Summary FT & T1993, (Second International Conference on Fuzzy Theory and Technology, Summary FT & T1993) 1993. p. .
  12. Generalized fuzzy set s and Representation of Incomplete Knowledge. Ren Ping . fuzzy set s and Systems, 1990. 1 p. .
  13. Introduction to fuzzy set s, W Pedrycz , F Gomide . 1998. Cambridge, MA: MIT Press.
Notes
1
© 2021 Global Journals
2
Fuzzy Reinforcement Learning using Neural Network: An Application to Medical Diagnosis and Business
3
Fuzzy Reinforcement Learning using Neural Network: An Application to Medical Diagnosis and Business Intelligence
Home 
Date: 2021-07-15